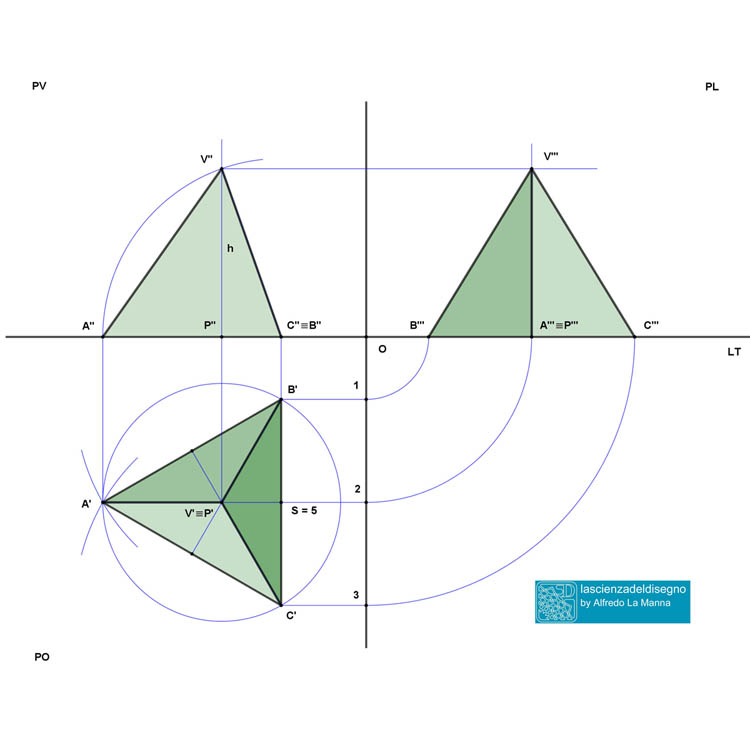
Proiezioni ortogonali di un tetraedro date le misure di uno spigolo

La rappresentazione di un tetraedro nelle proiezioni ortogonali non presenta particolari problemi. Il tetraedro é il solido più sempliece del ristretto gruppo dei poliedri regolari; é costituito da sole quattro facce triangolari equilatere, da sei spigoli uguali e da soli quattro vertici.
Gli altri poliedri regolari sono l’esaedro (o cubo), formato da sei facce quadrate uguali, l’ottaedro (otto facce), il dodecaedro (dodici facce) e l’icosaedro (venti facce). Ricordo che ognuno di questi poliedri rispetta le fondamentali proprietà di avere tutte le facce uguali ed anche tutti gli spigoli uguali.
Nel nostro caso rappresenteremo nelle proiezioni ortogonali un tetraedro con spigoli di dimensioni uguali a cinque unità, che nel nostro foglio da disegno potrebbero essere ad esempio cinque centimetri. Inoltre posizioneremo il solido in modo che una delle sue facce risulti poggiante sul piano orizzontale di proiezione, ed uno degli spigoli della sua sua base, ovvero quella coincidente con PO, deve essere ortogonale alla LT. Quest’ultima condizione renderà più facile la costruzione del solido e la sua rappresentazione.
Dopo aver suddiviso il nostro piano da disegno nei tre fondamentali piani di proiezione PO, PV e PL e conseguentemente aver individuato la linea di terra LT, cominceremo a disegnare sul PO proprio lo spigolo ortogonale alla LT, avendo cura di assegnare ad esso la lunghezza di cinque unità. Quindi, facendo centro sugli estremi C′ e B′ di tale spigolo, tracceremo due archi della stessa lunghezza dello spigolo suddetto che si intersecheranno nel punto A′, ovvero l’altro vertice della faccia di base del solido.
Una volta disegnata la faccia di base, individueremo l’ortocentro di essa, semplicemente tracciando dai tre vertici i tre segmenti perpendicolari al lato opposto; dato che si tratta in questo caso di facce tutte triangolari equilatere, tutti e tre questi segmenti individueranno il punto medio del lato opposto. Nell’ortocentro così trovato dovranno trovarsi i punti V′ e P′, rispettivamente la prima proiezione del vertice superiore del solido e il piede della perpendicolare da V alla faccia di base, ovvero l’altezza del tetraedro.
Per poter rappresentare il tetraedro in seconda proiezione sul PV occorre trovare l’altezza h del solido: a tal proposito possiamo immaginare di far coincidere temporaneamente la faccia inclinata del solido di vertici V, B e C, con la faccia coincidente col PO. In tal modo individueremo il vertice V ribaltato sul PO e coincidente con il vertice A. Possiamo dunque far compiere a V ribaltato una rotazione attorno allo spigolo di base di vertici B′ – C′, descrivendo un arco di cerchio che intersecherà l’altezza proprio nel vertice V in seconda proiezione, ovvero V″. Determinata la seconda proiezione V″ del vertice superiore, otterremo anche l’altezza h del solido.
Con il metodo consueto, tracciando dai vertici di base in prima proiezione le orizzontali fino alla verticale di separazione tra i piani, individueremo i punti 1, 2 e 3, dai quali tracceremo gli archi con centro in O fino ad intersecare la LT per trovare le terze proiezioni su PL del vertici di base A, B e C. Da P′′′ disegneremo successivamente la verticale fino ad intersecare l’orizzontale da V″ in modo da individuare la terza proiezione del vertice superiore V′′′ sul PL, completando così l’esercizio.