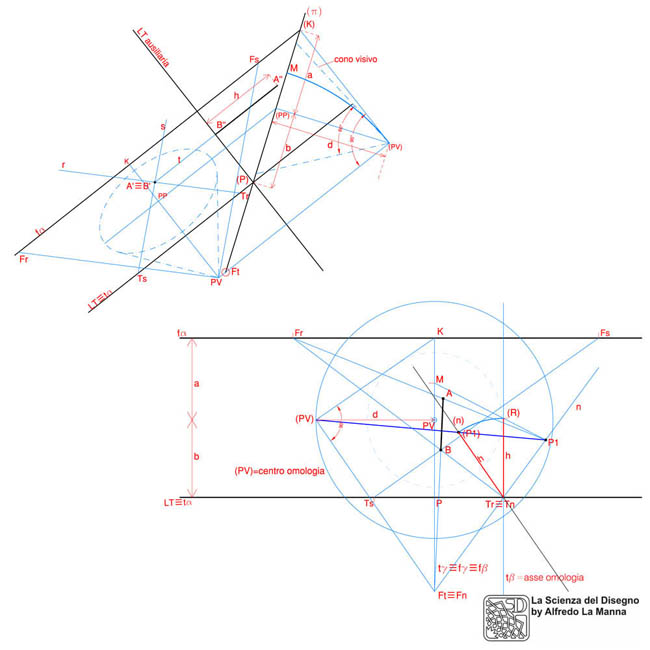
Prospettiva a quadro inclinato di un segmento verticale

L'esercitazione illustrata accanto è un caso semplice di prospettiva a quadro inclinato, molto istruttiva perché il procedimento descritto per rappresentare un semplice segmento ortogonale al piano geometrale, è anche utilizzato per trovare l'altezza dei solidi da rappresentare con quadro prospettico comunque inclinato rispetto al piano orizzontale α (piano geometrale).
Il disegno preparatorio è stato sviluppato nelle due viste orizzontale e di profilo, in modo da fissare sia l'altezza del punto di vista nonché le distanze a, b, dei rispettivi punti notevoli K e P (descritti in seguito), sia l'inclinazione dell'asse principale PV-PP rispetto alla verticale (o rispetto al geometrale). Nel caso di quadro prospettico inclinato, il punto principale PP non appartiene alla linea d'orizzonte LO, che nel disegno coincide con fα, retta di fuga del piano α.
Il segmento verticale è stato posizionato in modo da avere il vertice B inferiore coincidente col piano α; tale vertice è inoltre individuato dalla intersezione delle rette r ed s. Altri punti notevoli trovati nel disegno preparatorio sono il punto K, che giace sulla fα e sul piano proiettante γ (ortogonale al quadro e passante per PV) e il punto P, appartenente alla LT e allo stesso piano γ.
Nel disegno preparatorio sono state inoltre individuate le due fughe Fr ed Fs sulla LO e una terza fuga, molto importante, denominata Ft, che non appartiene alla LO ma alla fγ, fuga della retta t alla quale appartiene il segmento suddetto e di tutte le rette parallele a t che sono ortogonali al piano α geometrale.
Il disegno della restituzione prospettica comincia con il giusto posizionamento di tα e fα, fuga e traccia del geometrale, che devono essere distanti da PV rispettivamente delle quantità a, b. Ft viene individuata ribaltando sul quadro il punto di vista e tracciando la perpendicolare al segmento (PV)-K fino ad intersecare tγ coincidente con fγ. Si riportano anche ovviamente sulla fα le fughe Fr e Fs, mentre sulla tα le tracce Tr e Ts. Vedi anche il passo 13/26 del pdf multipagina, che ti consiglio di seguire per comprendere meglio i passaggi descritti.
Il punto M, riportato anche nella restituzione prospettica, viene determinato precedentemente nel disegno preparatorio semplicemente ribaltando sul quadro il punto PV facendolo ruotare attorno a Ft in modo da descrivere un arco nel piano γ. Si disegni adesso sul quadro un segmento di estensione uguale all'altezza h e di estremi (R) superiore e Tr quello inferiore, come descritto nel passo 18/26. Per comprendere meglio questa fase del procedimento ti consiglio di vedere anche i passaggi precedenti dal 15/26 al 17/26, dove il disegno preparatorio è stato rappresentato più in dettaglio. L'estremo superiore R è stato messo tra parentesi perché esso rappresenta il ribaltamento sul quadro dell'estremo superiore R di un segmento verticale con vertice inferiore coincidente con Tr, che risulta pertanto parallelo al segmento verticale che si vuole rappresentare in prospettiva. Questo segmento verticale, parallelo al segmento A-B da rappresentare, ribaltandosi sul quadro compierebbe un movimento di rotazione attorno al suo vertice inferiore con un angolo uguale a quello precedentemente ottenuto dal ribaltamento di PV per trovare il punto M. Tale ribaltamento dovrà compiersi lungo un piano β parallelo al piano γ (passo 17/26). Come si può notare, le rette v, u, passanti la prima da PV e M e la seconda da R e (R), sono rette parallele. Questo vuol dire che il punto M è anche il punto di fuga della retta u e di tutte le rette parallele ad essa.
Tenendo conto di quest'ultima constatazione, è lecito individuare sulla prospettiva della retta n, perpendicolare al piano geometrale α e con Tn ≡ Tr, il punto P1, prospettiva dell'estremo superiore R del segmento verticale sopra descritto (passo 20/26); del resto la congiungente M-(R)-P1 è anche la prospettiva della retta u descritta nel disegno preparatorio (passo 17/26), ricordando che essa deve convergere verso M, che rappresenta anche il suo punto di fuga, come già affermato in precedenza. Poichè la retta n ha la sua traccia sulla LT coincidente con la traccia Tr, è possibile collegare P1 con Fr e trovare per intersezione con la retta t, passante per il vertice di base B, il vertice superiore A del segmento in prospettiva (passo 22/26), completando in tal modo la rappresentazione del segmento A-B in prospettiva.
Se si immaginasse di ribaltare sul quadro la retta t in modo da farle compiere un movimento di rotazione attorno alla tβ mantenendo invariato l'angolo da essa formato con la traccia del suddetto piano, tale retta ribaltata (n) dovrà essere parallela alla congiungente (PV)-Fn. Individuando sulla n ribaltata il punto (P1), distante della quantità h da Tn, osserveremo che P1 in prospettiva, il suo corrispondente (P1) e il punto di vista ribaltato (PV), risultano essere esattamente allineati (passo 26/26) nella corrispondenza data dalla omologia piana con asse dell'omologia dato dalla tβ e centro dell'omologia coincidente con (PV). Questa è una ulteriore prova dell'esattezza del procedimento per individuare l'estremo superiore B del segmento in prospettiva.